题目
设有N个运动员要进行网球循环赛,设计一个满足以下要求的比赛日程表
- 每个选手必须与其他n-1个选手各赛一次;
- 每个选手一天只能赛一次;
- 当n 是偶数,循环赛进行n-1简单天,当n是奇数,循环赛进行n天。
分析
1. 首先考虑简单问题(n = 2^k)
这个我先上一个图大家应该就可以明白:
应该很容易想到分治法,有如下规律:对于任意一个正方形区域(包括4、16……个小方块)左上角和右下角相等,右上角和左下角相等(如果懒得看汉字就直接看上面几种颜色的方块吧)
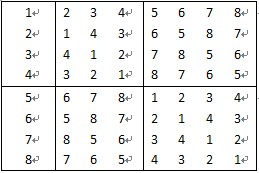
按分治策略,我们可以将所有的选手分为两半,则n个选手的比赛日程表可以通过n/2个选手的比赛日程表来决定。递归地用这种一分为二的策略对选手进行划分,直到只剩下两个选手时,比赛日程表的制定就变得很简单。这时只要让这两个选手进行比赛就可以了。如上图,所列出的正方形表是8个选手的比赛日程表。其中左上角与左下角的两小块分别为选手1至选手4和选手5至选手8前3天的比赛日程。据此,将左上角小块中的所有数字按其相对位置抄到右下角,又将左下角小块中的所有数字按其相对位置抄到右上角,这样我们就分别安排好了选手1至选手4和选手5至选手8在后4天的比赛日程。
然后这个代码也很容易:
- 非递归(k是2上面的次数)
void SetTable(int **a, int k) { //初始化左上角数 a[0][0] = 1; a[0][1] = 2; a[1][0] = 2; a[1][1] = 1; //然后分治安排 for(int i = 2; i <= k; i++) { int len = 1 << i; //len = 2^i int half = len / 2; //左下角子表就是左上角子表加上half for(int row = half; row < len; row ++) { for(int col = 0; col < half; col ++) { a[row][col] = a[row - half][col] + half; } } //右上角子表就是左下角子表 for(int row = 0; row < half; row ++) { for(int col = half; col < len; col ++) { a[row][col] = a[row + half][col - half]; } } //右下角子表就是左上角子表 for(int row = half; row < len; row ++) { for(int col = half; col < len; col ++) { a[row][col] = a[row - half][col - half]; } } } } - 递归(n是比赛总人数,这里先考虑简单的n = 2^k)
void tourna(int n, int **a) { if(n == 1) { a[0][0] = 1; return; } tourna(n/2, a); copy(n, a); } void copy(int n, int **a) { int m = n / 2; for(int i = 0; i < m; i++) { for(int j = 0; j < m; j++) { a[i + m][j + m] = a[i][j]; //右下角 a[i + m][j] = a[i][j] + m; //左下角 a[i][j + m] = a[i + m][j]; //右上角 } } }
2. 衍生到一般的偶数(如果n不是2的次方)
举一个例子(n=6),既然是分治法,按照大的思路,我们把tourna(6, a)问题转换成tourna(3, a)【这里的你们就先看成是上面的tourna函数】,那么问题又来了,n=3怎么解决呢?(自然引出了奇数的问题,那我们直接考虑下面的奇数问题,这里大家可以直接跳到第三种情况看,看完之后回看这一点)
我们可以将6分为(1 2 3)和(4 5 6)我们且看两者单独考虑的赛程:

- 考虑到(1 2 3)(4 5 6)“1和4”的第四列(第三天),只有一号选手和四号选手没比赛,那就让他们比,同理还有2和5,3和6,推出如下图【左图】
- 再来分析【右图】,第一行由于(1 5)(1 6)没比赛,后面就填他们,对应的也有(5 1)(6 1),再看第二行可以是(2 4)(2 6),由于6在第五天和1比赛了,所以应该是先填(2 6)然后(2 4),对应的也有(6 2)(4 2);后面同理。
其实我感觉这个就是找规律好吗,
和分治法有“桃子”关系
3. n为奇数
- 考虑到题目中有n天时间比赛,自然想到n = 4 的情况(看下图)
这个是4个人比赛3天的情况,现在如果只有3个人,那么岂不是正好是3天,我们仅仅需要将其中的4改变为0(看下图),代表选手那天空闲就可

- 其实对于一般的奇数,我们都可以转换成相应的n + 1,变成偶数再分治求解,最终递归到尽头就是n = 3(然后我们回到第二问)
最终代码
# include <iostream>
using namespace std;
void output(int **a, int n)
{
if(n % 2 == 1) //n为奇数时候的输出
for (int i = 0; i < n; i++)
{
for (int j = 0; j < n + 1; j++)
{
if(a[i][j] == n + 1)
cout << 0;
else cout << a[i][j];
if (j == n)
cout << endl;
else
cout << ' ';
}
}
else //n为偶数时候的输出
for (int i = 0; i < n; i++)
{
for (int j = 0; j < n; j++)
{
cout << a[i][j];
if (j == n - 1)
cout << endl;
else
cout << ' ';
}
}
}
void copy(int n, int **a)
{
int m = n / 2;
//cout << m << endl;
for(int i = 0; i < m; i++)
{
for(int j = 0; j < m; j++)
{
a[i + m][j + m] = a[i][j]; //右下角
a[i + m][j] = a[i][j] + m; //左下角
a[i][j + m] = a[i + m][j]; //右上角
}
}
}
void copyodd(int n, int **a)
{
int m = n / 2;
int *b = new int[n];
for(int i = 0; i < m; i++)
{
b[i] = m + i + 1; // 4 5 6
b[m + i] = b[i]; // 4 5 6
}
for(int i = 0; i < m; i ++)
{
for(int j = 0; j < m+1; j ++) //改写左上角和填写右下角
{ //这里如果你硬要说什么解释的话,我也说不出啥来,我看来就是找规律
if(a[i][j] > m)
{
a[i][j] = b[i];
a[m + i][j] = (b[i] + m) % n;
}
else a[m +i][j] = a[i][j] + m;
}
for(int j = 1; j < m; j++) //填写右上角和对应的右下角
{ //这里我当时是把 n = 6作为特例带进去一个一个是试出规律来的
a[i][m + j] = b[i + j];
a[b[i + j] - 1][m + j] = i + 1;
}
}
}
void makecopy(int n, int **a)
{
if((n/2 > 1) && ((n/2)%2 == 1)) copyodd(n, a);
else copy(n, a);
}
void tourna(int n, int **a)
{
if(n == 1)
{
a[0][0] = 1;
return;
}
if(n % 2 == 1)
{
tourna(n+1, a); //奇数+1变成偶数
return;
}
tourna(n/2, a); //分治
makecopy(n, a);
}
int main()
{
int n;
cin >>n;
int **a = new int *[2*n];
for(int i = 0; i < 2*n; i++) //分配空间
a[i] = new int[2*n];
tourna(n, a);
output(a, n);
for(int i = 0; i < 2*n; i ++) //delete空间
delete []a[i];
delete []a;
return 0;
}





